Focal Loss

Focal Loss는 2017년 말에 Fair(현 Meta AI Research)에서 발표한 논문 ‘Focal Loss for Dense Object Detection’에서 소개되었으며 현재 Object Detection 모델중 1 stage detector(YOLO, SSD)와 같이 anchor box를 활용해 dense prediction을 하는 모델들은 현재까지 사용하고 있는 loss function이다.

논문에서는 Focal Loss를 적용한 RetinaNet이라는 모델을 소개하지만 이번 포스팅에는 Focal Loss의 핵심 개념을 이해하고 loss function을 구현해보려고 한다.

---

1. Limit Of Cross Entroy Loss 

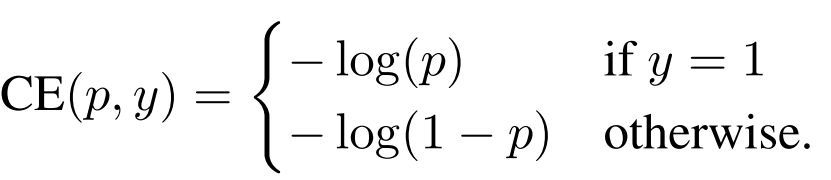
• Binary Cross Entropy loss는 위 식을 통해 계산이 된다. Cross Entropy는 모델이 잘 한 것에 대해서 보상을 주는 방식이 아닌 잘못한 것에 대해 벌을 주는 방식(loss)으로 모델을 학습하도록 유도한다.

• 위 식에서 p는 sigmoid를 통과해 0~1사이의 값을 가지는 모델의 예측 확률값이다. 잘 학습된 모델일수록 정답에 대해(y=1) p는 1에 가까운 값이 나오고 정답이 아닐때(otherwise) p는 0에 가까운 값이 나온다. (-log(1) = 0

  -log(0) = ∞)

• 위 Binary Cross Entropy식을 Cross Entropy처럼 하나의 식으로 표현하기 위해 아래와 같이 정리할 수 있다.

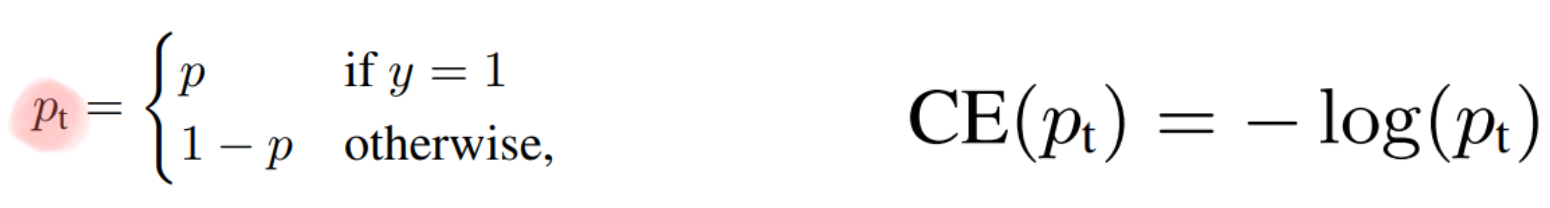
• y=1 일때 와 otherwise일 때의 확률값 p와 p-1을 pt로 치환해 하나의 식으로 표현하였다. 
• 예를 들어 만약 학습된 모델이 정답 데이터에 대해 p=0.98, 정답이 아닌 데이터에 대해 p=0.02라고 예측을 했다면 loss는 아래와 같이 계산된다.

• True: -log(0.98) = 0.00877

  False: -log(1-0.02) = 0.00877

• 정답과 정답이 아닌 데이터의 loss가 같음을 알 수 있으며 결국 pt값이 클 수록 좋은 모델이라고 할 수 있다.

그런데 일반적인 Cross Entropy에는 치명적인 단점이 있다. 바로 class unbalance를 고려하지 않는다는 것이다. Object Detection에서 위에서 언급한 1 stage detector들은 대부분 한장의 이미지에 대해 소수의 객체에 대한 예측과 수천, 수만개의 background 예측이 존재하기 때문에 정답이 아닌(background) 예측값들이 비정상적으로 많다.

하지만 위의 예제처럼 일반적인 Cross Entropy는 정답과 정답이 아닌 데이터의 loss가 비슷하기 때문에 엄청나게 많은 background로 인해 background에 대한 loss가 누적되어 정답에 대한 loss를 압도하면서 우리에겐 불필요한 background에 대해 학습이 집중되는 문제가 발생한다.

이 문제를 해결하기 위해 Balanced Cross Entropy라는 것이 존재한다.

2. Limit Of Balanced Cross Entropy

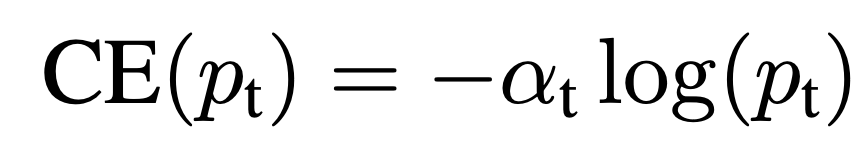
• 위 식은 Cross Entropy의 class unbalnce에 대한 문제를 잡기위해 log앞에 αt라는 hyperparameter를 추가한 Balanced Cross Entropy 식이다.
• αt는 pt와 마찬가지로 정답일땐 α 정답이 아닐땐 α-1로 계산하면 된다. 예를들어 위 상황과 마찬가지로 p=0.98 추가적으로 α=0.80이라면 losss는 아래와 같이 계산된다.

• True: -0.8log(0.98) = 0.007016

  False: -(1-0.8)log(1-0.02) = 0.001754

• negative example(background)에 대한 loss를 positive example에 대한 loss보다 훨씩 작게 만들어 조금 더 positive example에 집중할 수 있게된다.

하지만 Balanced Cross Entropy에서도 해결할 수 없는 문제가 하나 더 있다. positive/negative example에 대한 문제를 해결했지만 easy/hard example을 구분할 수 없다는 것이다.

여기서 background 혹은 검출하기 쉬운 물체는 예측을 잘 하기 때문에 easy example이라고 하며 검출하기 어려운 물체를 hard example이라고 한다. Balanced Cross Entropy는 True와 False에 대한 loss를 다르게 구성하기 때문에 이러한 문제를 해결할 수 없었으며 Focal Loss라는 개념을 도입하면서 문제를 해결할 수 있었다.

3. Focal Loss

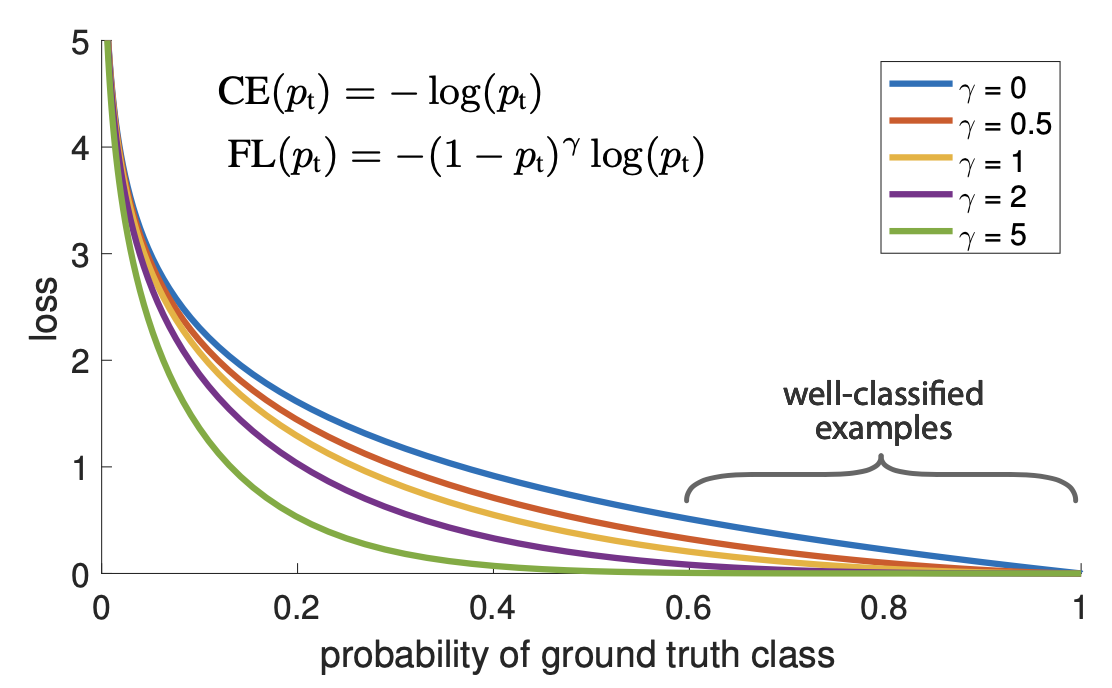
• 위 그래프에서 파란색 선(γ=0)이 일반적인 Cross Entropy Loss이고 나머지 선들이 Focal Loss이다. FL선들이 CE선보다 아래에 있는것을 보아 Loss자체는 FL이 더 낮다는 것을 알 수 있다.
• 그래프에서 중요하게 봐야할 점은 CE대비 FL에서 예측확률값(x축)이 낮을때에 비해 확률이 높아질수록 loss값이 급격하게 낮게 설정된다는 것이다. 즉 확률이 높을수록(easy example) 낮은 loss, 확률이 낮을수록(hard example) 비교적 큰 loss를 갖게 되는 것이다.
• 이를 식으로 표현한 것이 그래프에 있는 FL식이며 Focal Loss는 Cross Entropy 식에서 −(1−pt)γ 텀만 추가되었다.
• γ 값을 조정하여 easy/hard example간의 loss 격차를 조절할 수 있는데 논문에서는 실험을 통해 γ=2일때 가장 효과적이었다고 한다.
• 예시로 pt=0.98일때(easy)와 pt=0.2(hard)일때 Focal Loss를 계산해보자

• pt=0.98: -(1-0.98)^2 x log(0.98) = 0.000003508

  pt=0.2: -(1-0.2)^2 x log(0.2) = 0.44734

이처럼 논문에서는 Focal Loss를 통해 Dense Prediction을 하는 Object Detector의 loss function을 재구성하여 기존보다 높은 성능으로 끌어올리는데 성공하였고 Balanced Cross Entropy의 αt를 추가하는 것이 조금 더 성능이 높았다고 한다. 그러므로 최종 식은 아래와 같다. 

---

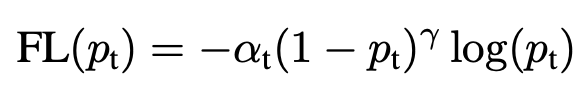
Pytorch Implementation

import torch
import torch.nn as nn

class FocalLoss(nn.Module):
    def __init__(self, gamma=2, alpha=0.25):
        super(FocalLoss, self).__init__()
        self.loss_fn = nn.BCEWithLogitsLoss()
        self.gamma = gamma
        self.alpha = alpha
        self.reduction = self.loss_fn.reduction  # mean, sum, etc..

    def forward(self, pred, true):
        bceloss = self.loss_fn(pred, true)

        pred_prob = torch.sigmoid(pred)  # p  pt는 p가 true 이면 pt = p / false 이면 pt = 1 - p
        alpha_factor = true * self.alpha + (1-true) * (1 - self.alpha)  # add balance
        modulating_factor = torch.abs(true - pred_prob) ** self.gamma  # focal term
        loss = alpha_factor * modulating_factor * bceloss  # bceloss에 이미 음수가 들어가 있음

        if self.reduction == 'mean':
            return loss.mean()
        
        elif self.reduction == 'sum':
            return loss.sum()
        
        else:  # 'none'
            return loss

---

End

지금까지 Dense Object Detection에서 사용하는 loss인 Focal Loss에 대하여 알아보았다.

Focal loss는 단순히 Dense Prediction의 class imbalance 문제만 해결하는 것이 아닌 easy, hard example까지 고려하여 loss의 가중치를 다르게 가져갈 수 있도록 해주며 지금까지도 많이 사용되는 loss function이다.

2022년 새해가 밝았다. 여러가지 딥러닝 프로젝트를 진행할수록 전체적인 머신, 딥러닝 프로세스를 한번에 관리할 수 있는 MLOps의 필요성을 느꼈다. 모델이 발전하는 것도 중요하지만 MLOps가 제대로 구축이 되었을때 다양한 도메인에서 AI 도입이 빠르게 증가 할 것이라고 생각한다. 올해는 계속해서 최신 딥러닝 연구들을 주의깊게 지켜보는 동시에 MLOps를 깊게 파헤쳐 보려고 한다.

Keep going

Reference

paper - https://arxiv.org/abs/1708.02002