Batch Normalization
이번 포스팅에서는 Batch Normalization에 대해 알아보려고 한다. 레이어 수가 많이질수록 즉 망이 깊어질수록 vanishing/exploding gradient 문제로 인해 학습이 잘 되지 않았고 그것을 해결하기위해 activation function 변경, dropout, regularization 방법 등이 제시 되었지만 여전히 골칫거리로 남아있었다.
이 문제를 해결하기 위해 나온것이 이전 포스팅에서 다룬 ResNet 과 Batch Normalization이다. 천천히 Batch Normalization에 대해 알아보자.
What is vanishing / exploding gradient ?
vanishing gradient : 학습과정에서 backpropagation을 하면서 gradient가 앞쪽으로 전달되면서 업데이트를 하게 되는데 활성함수로 sigmoid나 hyper-tangent 같은 비선형 포화함수(non-linear saturating function)를 사용하게 되면 미분값이 0근처로 가게 되면서 backprop이 되지 않는 현상을 말한다.
exploding gradient : 이 경우는 미분값을 계산할때 너무 큰값 혹은 NAN 값이 나오는 경우를 말한다.
solution?
- Change activation function : sigmoid or hyper-tangent -> Relu(2011) - Careful initialization : 초기 weight값을 잘 설정하는 것. (ex. xavier initialization) - small learning rate : lr을 줄이면 gradient exploding 문제를 완화 시킬 수 있다.
하지만 이런 방법들은 간접적인 회피이고 본질적인 해결책이 아니기 때문에 망이 깊어지면 여전히 문제가 된다.
Internal Covariate Shift
internal covariate shift 란 학습과정에서 이전 레이어의 파라미터의 변화로 인해 현재 레이어 입력의 분포가 바뀌는 현상을 말한다. 레이어가 깊어지면 깊어질수록 당연히 Internal covariate shift가 심해지게 될 것이다. 이런 현상을 줄이기 위해서는 입력값에 대해 Normalize를 하는 방법을 들 수가있다.
Batch Normalization
Normalization은 원래 training 전체 집합에 대하여 실시를 하는 것이 최고의 효과를 거둘 수 있다. 하지만 computational cost로 인해 학습을 batch단위로 해야하기 때문에 Normalization도 batch 단위로 이루어져야 할 것이다. mini-batch SG 방식을 사용하게 되면, 파라미터의 update가 mini-batch 단위로 일어나기 때문에 그 mini-batch 단위로 BN을 실시한다. 여기서 mini-batch는 그안에서 correlation이 적어서 각각의 mini-batch들이 전체 데이터를 대표할 수 있도록 해야 한다.

논문에서는 위의 그림과 같이 학습에 대한 BN을 정의하였다. Normalize는 각각의 값에 평균을 빼주고 그것을 표준편차로 나눠주게 되는데 분모에있는 e(입실론)은 분모가 0이 되는것을 막기 위해 아주 작은 값으로 되어 있는 상수이다.
이렇게 되면 Normalize된 데이터들의 분포는 -1~1의 범위를 가지게 된다.
그리고 BN이 일반적인 Whitening기법(그냥 정규화만 하는 기법)과 다른 점은 바로 scale 과 shift 연산을 위한 γ와 β가 있다는 것이다. γ와 β가 있는 이유는 BN으로 데이터를 계속해서 normalize 해주게 되면 activation function의 non-linearty 성질을 잃게되는데 이것을 완화 시킬 수 있기 때문이다. 게다가 γ와 β가 추가됨으로써 정규화 시켰던 부분을 원래대로 돌리는 identity mapping도 가능하고, 학습을 통해 γ와 β를 정할 수 있기 때문에 단순하게 정규화 만을 할 때보다 훨씬 강력해진다.
나중에 코드에서 다시 설명 하겠지만 BN은 evaluation 할때는 조금 다르게 적용을 하여야 한다. evaluation 할때도 training과 마찬가지로 보통 batch_size를 가지고 진행을 하는데 batch_size가 8이라고 가정해보자. BN을 적용하기 위해서는 해당 batch 데이터들의 평균과 분산을 계산해야 하는데 만약 마지막 2개의 데이터가 바뀌게 된다면 위에 있던 6개의 데이터는 이전과 여전히 같은 데이터임에도 불구하고 평균과 분산이 이전과 달라지게 되면서 모델이 다른 결과를 낼 수 있기 때문이다. 그래서 BN은 train과 evaluation 에서 사용을 따로 둔다.
학습을 할때 각각의 Batch에서 계산했던 sample mean과 sample variance를 가지고 learning mean, learning variance로 만들어 준다. 즉 평균의 평균 그리고 분산의 평균을 저장해둔다는 의미이다. 그렇게 생긴 learning mean과 learning variance는 데이터에 분포에 상관없이 고정된 값이 되고 이 값들을 inference(evaluation)의 BN에서 평균과 분산으로 사용을 하여 정규화된 x를 얻게 된다.
그 다음에 정규화된 x에 training에서 학습이 된 γ를 곱하고 β를 더해주게 되면 inference 단계에서의 BN을 적용이 되고 이렇게 되면 batch안에서 데이터가 달라져도 같은 데이터에 대해서는 같은 output을 낼 수 있게 된다.
BN을 사용했을때와 사용하지 않았을때의 성능 비교
사용한 데이터 : Mnist(28x28x1(grey scale))
BN기법의 유무에 따른 성능을 빠르게 파악하기 위해 모델은 간단한 MLP로 구성
Import and define parameter
import torch
import torchvision
import torch.nn as nn
import torchvision.transforms as transforms
import matplotlib.pyplot as plt
device = 'cuda' if torch.cuda.is_available() else 'cpu'
learning_rate = 0.01
training_epochs = 10
batch_size = 32
사용된 파라미터는 위의 코드와 같다.
Load the Data
train_dataset = torchvision.datasets.MNIST(root='./data',train=True,
transform=transforms.ToTensor(), download=True)
test_dataset = torchvision.datasets.MNIST(root='./data', train=False,
transform=transforms.ToTensor(), download=True)
trainloader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True, drop_last=True)
testloader = torch.utils.data.DataLoader(test_dataset, batch_size=batch_size, shuffle=False, drop_last=True)
Define Model
# nn layers
linear1 = torch.nn.Linear(784, 32, bias=True)
linear2 = torch.nn.Linear(32, 32, bias=True)
linear3 = torch.nn.Linear(32, 10, bias=True)
relu = torch.nn.ReLU()
bn1 = torch.nn.BatchNorm1d(32)
bn2 = torch.nn.BatchNorm1d(32)
nn_linear1 = torch.nn.Linear(784, 32, bias=True)
nn_linear2 = torch.nn.Linear(32, 32, bias=True)
nn_linear3 = torch.nn.Linear(32, 10, bias=True)
# model
bn_model = torch.nn.Sequential(linear1, bn1, relu,
linear2, bn2, relu,
linear3).to(device)
nn_model = torch.nn.Sequential(nn_linear1, relu,
nn_linear2, relu,
nn_linear3).to(device)
3개의 Linear 레이어를 이어 붙여 하나는 BN이 들어간 모델 나머지 하나는 단순히 BN이 없는 모델을 정의
define cost/loss & optimizer
criterion = torch.nn.CrossEntropyLoss().to(device) # Softmax is internally computed.
bn_optimizer = torch.optim.Adam(bn_model.parameters(), lr=learning_rate)
nn_optimizer = torch.optim.Adam(nn_model.parameters(), lr=learning_rate)
Train and Evaluate
train_losses = []
train_accs = []
valid_losses = []
valid_accs = []
train_total_batch = len(trainloader)
test_total_batch = len(testloader)
for epoch in range(training_epochs):
bn_model.train() # set the model to train mode
for X, Y in trainloader:
# reshape input image into [batch_size by 784]
# label is not one-hot encoded
X = X.view(-1, 28 * 28).to(device)
Y = Y.to(device)
bn_optimizer.zero_grad()
bn_prediction = bn_model(X)
bn_loss = criterion(bn_prediction, Y)
bn_loss.backward()
bn_optimizer.step()
nn_optimizer.zero_grad()
nn_prediction = nn_model(X)
nn_loss = criterion(nn_prediction, Y)
nn_loss.backward()
nn_optimizer.step()
with torch.no_grad():
bn_model.eval() # set the model to evaluation mode
# Test the model using train sets
bn_loss, nn_loss, bn_acc, nn_acc = 0, 0, 0, 0
for i, (X, Y) in enumerate(trainloader):
X = X.view(-1, 28 * 28).to(device)
Y = Y.to(device)
bn_prediction = bn_model(X)
bn_correct_prediction = torch.argmax(bn_prediction, 1) == Y
bn_loss += criterion(bn_prediction, Y)
bn_acc += bn_correct_prediction.float().mean()
nn_prediction = nn_model(X)
nn_correct_prediction = torch.argmax(nn_prediction, 1) == Y
nn_loss += criterion(nn_prediction, Y)
nn_acc += nn_correct_prediction.float().mean()
bn_loss, nn_loss, bn_acc, nn_acc = bn_loss / train_total_batch, nn_loss / train_total_batch, bn_acc / train_total_batch, nn_acc / train_total_batch
# Save train losses/acc
train_losses.append([bn_loss, nn_loss])
train_accs.append([bn_acc, nn_acc])
print(
'[Epoch %d-TRAIN] Batchnorm Loss(Acc): bn_loss:%.5f(bn_acc:%.2f) vs No Batchnorm Loss(Acc): nn_loss:%.5f(nn_acc:%.2f)' % (
(epoch + 1), bn_loss.item(), bn_acc.item(), nn_loss.item(), nn_acc.item()))
# Test the model using test sets
bn_loss, nn_loss, bn_acc, nn_acc = 0, 0, 0, 0
for i, (X, Y) in enumerate(testloader):
X = X.view(-1, 28 * 28).to(device)
Y = Y.to(device)
bn_prediction = bn_model(X)
bn_correct_prediction = torch.argmax(bn_prediction, 1) == Y
bn_loss += criterion(bn_prediction, Y)
bn_acc += bn_correct_prediction.float().mean()
nn_prediction = nn_model(X)
nn_correct_prediction = torch.argmax(nn_prediction, 1) == Y
nn_loss += criterion(nn_prediction, Y)
nn_acc += nn_correct_prediction.float().mean()
bn_loss, nn_loss, bn_acc, nn_acc = bn_loss / test_total_batch, nn_loss / test_total_batch, bn_acc / test_total_batch, nn_acc / test_total_batch
# Save valid losses/acc
valid_losses.append([bn_loss, nn_loss])
valid_accs.append([bn_acc, nn_acc])
print(
'[Epoch %d-VALID] Batchnorm Loss(Acc): bn_loss:%.5f(bn_acc:%.2f) vs No Batchnorm Loss(Acc): nn_loss:%.5f(nn_acc:%.2f)' % (
(epoch + 1), bn_loss.item(), bn_acc.item(), nn_loss.item(), nn_acc.item()))
print()
print('Learning finished')
torch.argmax(1)을 하면 x축에서의 즉 10개의 class의 값중에 가장 큰 값의 인덱스를 반환해주고 조건문이 있으므로 boolean(True or False)를 반환한다.
그리고 그 텐서들을 .float()을 하게되면 True값은 1.0, False값은 0.0 이 되고 .mean을 하므로 해당 batch의 정확도를 얻을 수 있다.
위 코드를 실행한 결과는 아래와 같다.
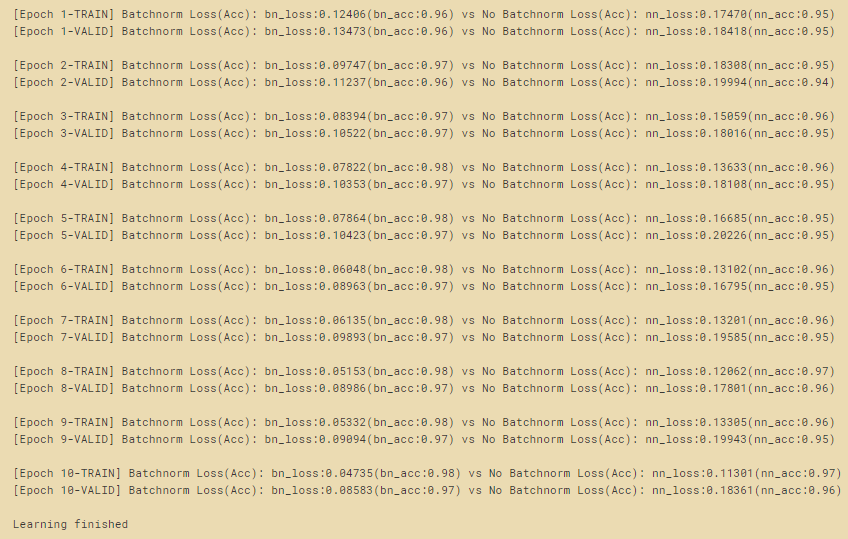
Visualization
def plot_compare(loss_list, ylim=None, title=None) -> None:
bn = [i[0] for i in loss_list]
nn = [i[1] for i in loss_list]
plt.figure(figsize=(8,5))
plt.plot(bn, label='With BN')
plt.plot(nn, label='Without BN')
if ylim:
plt.ylim(ylim)
if title:
plt.title(title)
plt.legend()
plt.grid('on')
plt.show()
plot_compare(train_losses, title='Training Loss at Epoch')
plot_compare(train_accs, [0, 1.0], title='Training Acc at Epoch')
plot_compare(valid_losses, title='Validation Loss at Epoch')
plot_compare(valid_accs, [0, 1.0], title='Validation Acc at Epoch
시각화를 위한 간단한 함수를 정의 하였고 위 코드를 실행한 결과는 아래와 같다.
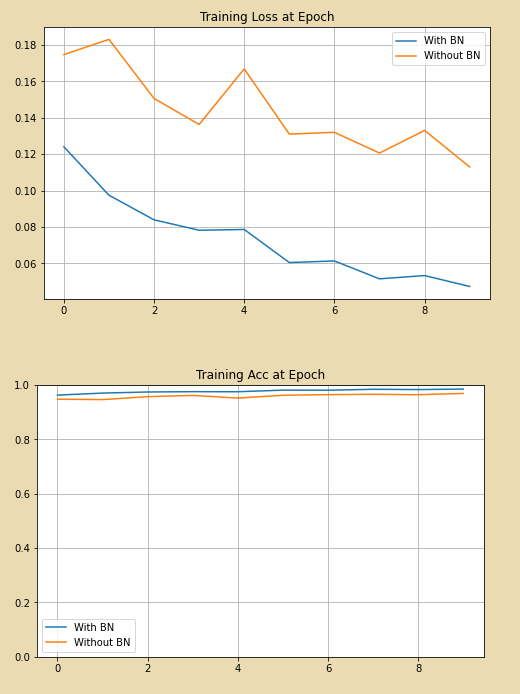
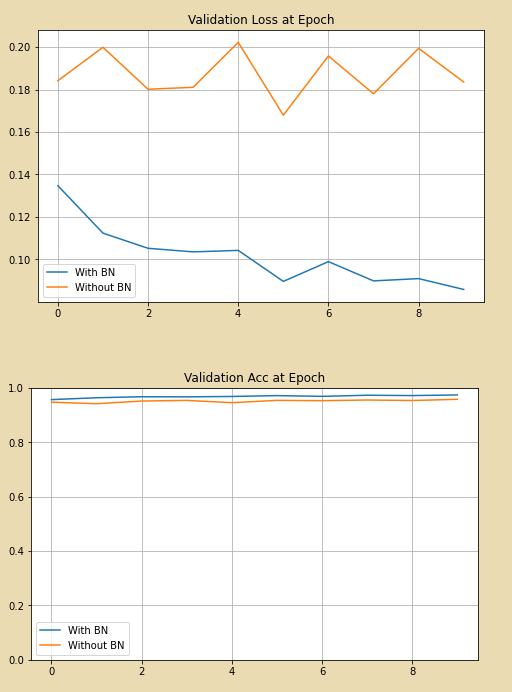
위쪽 그래프는 loss 그래프이며 확실히 BN을 사용한 모델의 성능이 BN을 사용하지 않은 모델의 성능보다 좋다는 것을 알 수 있다.
아래쪽 그래프는 Accuracy 그래프 이다. MNIST 이미지 자체가 간단하기 때문에 보통 딥러닝으로 구현을 하면 정확도가 높게 나오지만 자세히 보면 그래도 BN을 적용 하였을 때의 정확도가 약 1~2% 정도 높은것을 확인 할 수가 있다.
ENDING
이번 포스팅에서는 Batch Normalization에 대해 알아보았다. BN은 Internal Covariate Shift 문제를 해결할 수 있으며, 이를 통해 딥러닝의 고질적인 문제들이 해결 가능하게 되었다. Vanishing / exploding gradient 문제의 해결책이 생기면서 lr을 낮춰야 하는 상황이 필요가 없어졌기 때문에 lr을 높임으로써 초기 학습 속도의 향상은 물론 학습의 정확도까지 개선할 수 있게 되었다. BN이 나온 이후로 대부분의 모델에서 BN의 사용은 권장이 아닌 필수가 된 것 같다.

Leave a comment