[논문리뷰] Swin Transformer
Swin Transformer: Hierarchical Vision Transformer using Shifted Windows
Ze Liu† / Yutong Lin† / Yue Cao / Han Hu / Yixuan Wei† / Zheng Zhang / Stephen Lin / Baining Guo /
Microsoft Research Asia
이번 포스팅에서는 2021년 3월에 마이크로소프트(아시아)에서 발표한 Swin Transformer에 대해 알아보려고 한다. 해당 논문은 ViT에서 모든 patch가 self attention을 하는 것에 대한 computation cost를 지적하면서 각 patch를 window로 나누어 해당 윈도우 안에서만 self attention을 수행하고 그 윈도우를 한번 shift하고 다시 self attention을 하는 구조를 제시한다. (그래서 이름이 Swin (shifted windows) Transformer이다.)
또한 일반적인 Transformer와 달리 마치 Feature Pyramid Network같은 Hierarchical 구조를 제시하면서 classification은 물론 Object Detection, Segmentation에서 backbone으로 사용되어 좋은 성능을 내게 된다. Let’s dig in
Introduction
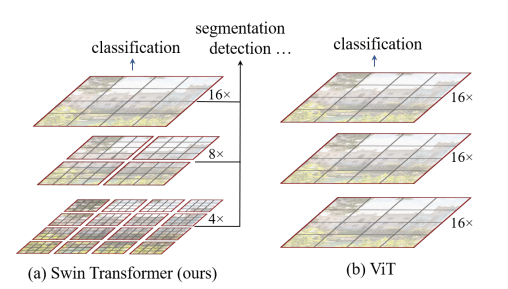
- 입력 이미지 사이즈가 224x224라고 생각해보자.
- ViT는 각 패치 사이즈를 16pixel x 16pixel으로 만들어 총 224/16 ** 2 = 196개의 patch를 가진 상태를 유지하고 각 patch와 나머지 전체 patch에 대한 self-attention을 수행한다. (quadratic computational complexity to image size)
- 반면에 Swin Transformer에서는 마치 feature pyramid network처럼 작은 patch 4x4에서 시작해서 점점 patch들을 merge 해나가는 방식을 취한다.
- 그림을 보면 빨간선으로 patch들이 나누어져 있는것을 볼 수 있는데 이것을 각각 window라고 부르고 Swin Transformer는 window내의 patch들끼리만 self-attention을 수행한다. (linear computational complexity to image size)
- 논문에서는 각 window size(M)을 7x7로 한다. 정리하면 첫번째 레이어에서 4x4 size의 각 patch가 56x56개가 있고 이것을 7x7 size의 window로 나누어 8x8개의 window가 생긴다.
- 즉 첫번째 stage에서 각 patch는 16개의 pixel이 있고 각 윈도우에는 49개의 patch가 있다는 의미 (사실 embedding을 하기 때문에 채널을 곱해줘야 하는데 그림의 이해를 돕기위해 채널은 곱하지 않았음)
Method
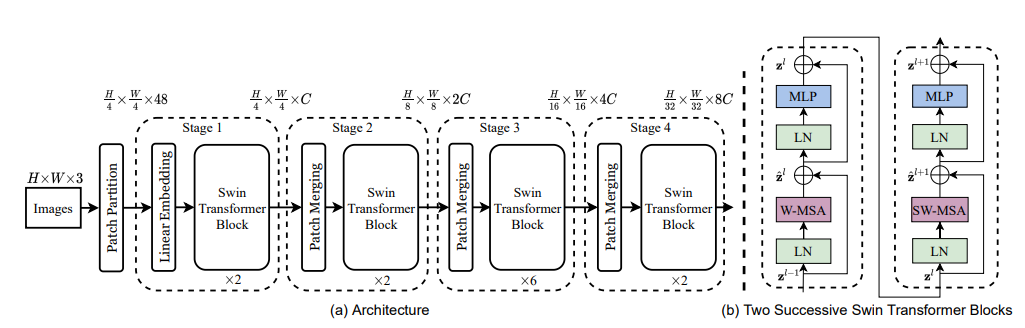
- 위 그림은 Swin Transformer 전체적인 구조이다. 크게 Patch Partition, Linear Embedding, Swin Transformer, Path Merging으로 구분이 되며 4개의 Stage로 이루어져 있다.
- 핵심 아이디어인 Swin Transformer Block은 오른쪽 그림(b)에 보이는 것과 같이 두개의 encoder로 구성되어 있으며 일반적인 MSA(Multi head Self-Attention)이 아니라 W-MSA, SW-MAS로 이루어져 있다.
- 각 stage 아래에 적혀있는 x2/x2/x6/x2 은 Swin Transformer Block의 횟수인데 1개의 Block당 2개의 encoder가 붙어 있으므로 세트로 묶어서 실제로는 1/1/3/1 개의 Block이 반복된다고 보면 된다.
- 각 stage 위에 적혀있는 H/4 x W/4 x C 는 patch x patch x channel이며 48은 초기 patch size x channel (4x4x3)으로 구해졌으며 C는 base model인 Swin-T에서 96을 사용한다.
Patch Partition, Patch Merging, Linear Embedding
위 그림에서 Patch Partition과 Patch Merging이 따로 구분되어 있는데 사실 이미지에서 Patch로 Partition하는 것과 Patch를 Merging하는것은 같은 일을 하는 것이기 때문에 같은 의미라고 볼 수 있다.
Stage 1 : Patch Partition/Merging
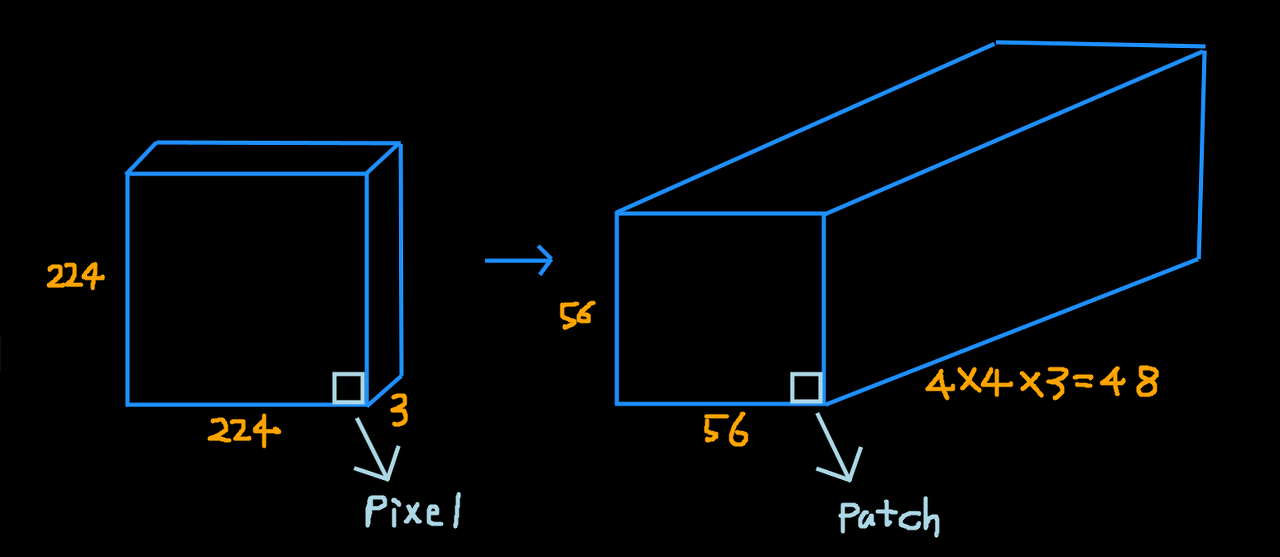
- 처음 input image에 Patch Partition을 하게되면 위 그림과 같이 변하게 된다.
- 여기서 중요한 것은 이미지에서 한 점은 pixel이지만 Patch Partition을 하게되면 한 점이 patch가 되고 각 patch의 픽셀정보들이 channel이 된다.
Stage 1: Linear Embedding
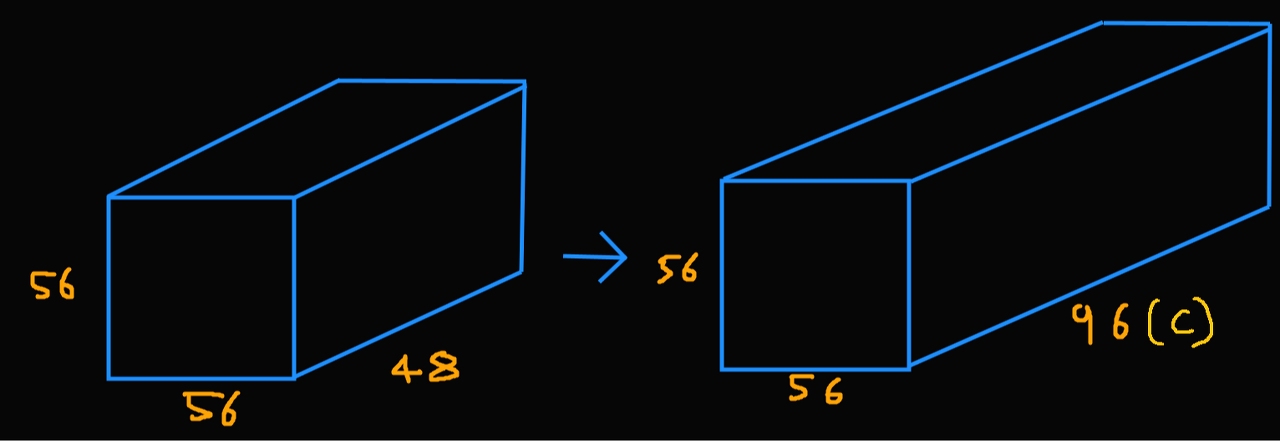
- Patch Partition 혹은 Patch Merging 이후에 Linear layer를 거쳐서 C의 dimension으로 만들어준다. C는 Tiny model 기준으로 stage마다 96, 192, 384, 768 로 이루어져 있다.
- 그림만 보면 1x1 convolution인것으로 착각할 수 있지만 단지 이해를 위한 그림이고 실제로 nn.Linear 연산으로 값을 변환한다.
Swin Transformer Block (Shifted Window based Self-Attention)
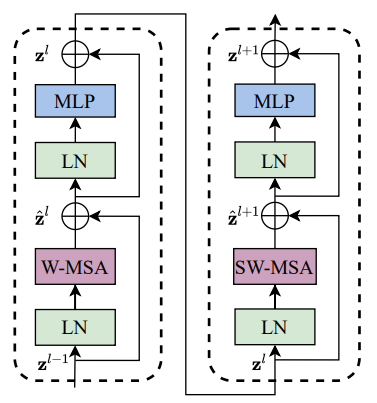
하나의 Block에는 두개의 Encoder로 구성이 되어있으며 ViT와 다른점은 기존에 사용하던 MSA가 아니라 Windows-MSA, Shifted Windows-MSA라는 점이다.
먼저 일반적인 MSA와 W-MSA는 무슨 차이점이 있고 이것이 왜 가능할까?
W-MSA는 현재 윈도우에 있는 패치들끼리만 self-attention 연산을 수행한다. 이미지는 주변 픽셀들끼리 서로 연관성이 높기 때문에 윈도우 내에서만 self-attention을 써서 효율적으로 연산량을 줄이려는 아이디어이다. (마치 CNN의 kernel을 쓰는 이유와 비슷)
논문에서는 W-MSA를 통해 일반적인 MSA의 quadratic한 연산을 linear 하게 만들어 줄 수 있다고 한다.
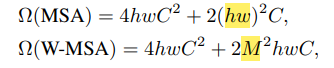
위 식 처럼 M(window size)은 hw(image size)에 비해 훨씬 작기 때문에 W-MSA의 연산량이 훨씬 적고 결국 image size가 커져도 ViT에 비해 연산량을 많이 줄일수있게 된다.
하지만 윈도우가 고정되어 있기 때문에 고정된 부분에서만 self-attention을 수행하는 단점이 있어서 저자들은 이 윈도우를 shift해서 self-attention을 한번 더 수행하였고 이것이 바로 SW-MSA이다.
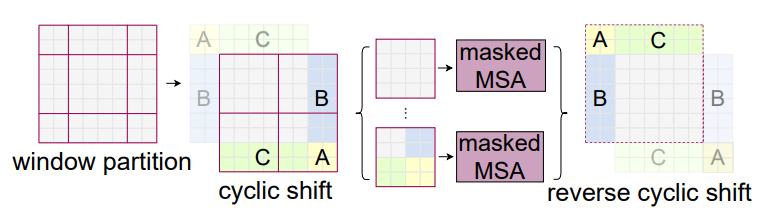
- SW-MSA는 위 그림과 같이 수행된다.
- 먼저 window를 shift시키는데 이것을 cyclic shift라고 부른다. window size // 2 만큼 우측 하단으로 shift하고 A,B,C구역을 mask를 씌워서 self-attention을 하지 못하도록 한다.
- 그 이유는 원래 ABC 구역은 좌상단에 있었던 것들이기 때문에 반대편에 와서 self-attention을 하는 것은 의미가 별로 없기 때문
- 마스크 연산을 한 후에는 다시 원래 값으로 되돌린다. (reverse cyclic shift)
- 결과적으로 SW-MSA를 통해서 윈도우 사이의 연결성을 나타낼 수 있다.
- 참고로 cyclic shift대신 padding을 사용해 마스킹을 대신할 수 있지만 저자들은 이 방법은 computation cost를 증가시키기 때문에 택하지 않았다고 한다.
Relative position bias
Swin Transformer는 ViT와 다르게 처음에 Position embedding을 더해주지 않았다. 대신 self-attention 과정에서 relative position bias를 추가하는데 이게 무엇일까?
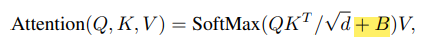
위 식을 보면 기존 ViT에서 softmax를 취하기 전에 B를 더하는 것을 볼 수 있는데 이것이 바로 Relative position bias이다. 기존에 position embedding은 절대좌표를 그냥 더해주었는데 본 논문에서는 상대좌표를 더해주는 것이 더 좋은 방법이라고 제시한다.
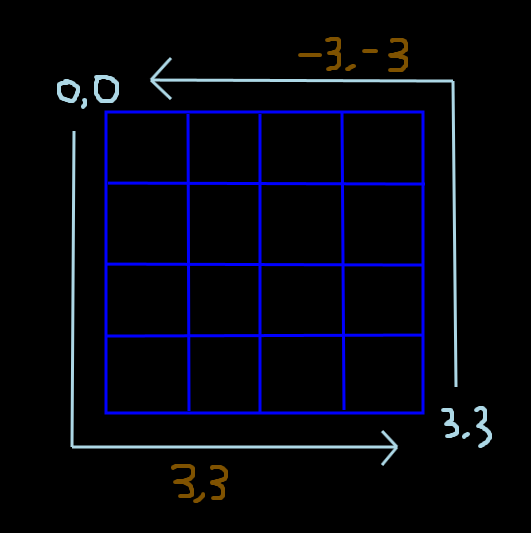
- 예를들어 위와같은 4x4 픽셀이 있을때 0,0 픽셀에서 3,3 픽셀로 이동을 하기 위해서는 3,3만큼 이동해야 한다.
- 하지만 반대로 3,3 에서 0,0 으로 가기 위해서는 -3,-3을 가야하기 때문에 어떤 픽셀을 중심으로 하냐에 따라서 이동해야하는 값이 달라지게 된다.
- 그렇기 때문에 단순하게 sin cos의 주기로 구한 절대좌표를 사용하는 것 보다 상대적인 좌표를 embedding해서 더해주는 것이 좋다고 한다.
Experiments
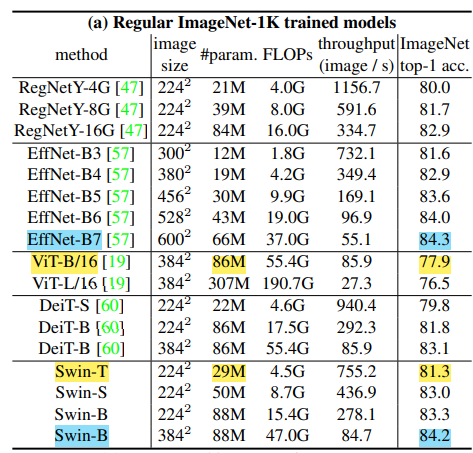
- ImageNet dataset에 대해 ViT base model보다 파라미터 수는 훨씬 적지만 성능은 3.4%가 높다. (노란색)
- CNN기반 모델중 가장 SOTA model인 EffcientNet-B7 과 대등할 정도의 성능을 보였다. (하늘색)
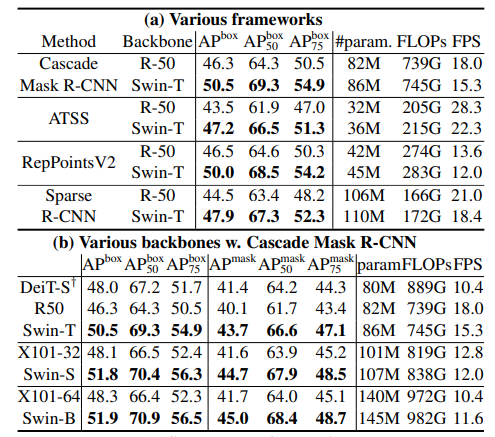
- 다른 Task(Object Detection, Segmentation 등)의 backbone으로 사용했을때의 성능은 거의 다 SOTA를 찍은 것을 볼 수 있다.
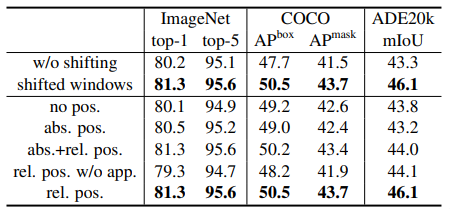
- SW-MSA없이 W-MSA만 사용했을때보다 둘다 사용했을때의 성능이 더 좋았고 abs positition embedding(기존에 사용하던 절대좌표) 과 relative postition embedding을 둘 다 쓰는 것 보다 relative postition embedding 하나만 사용하는 것이 제일 좋았다고 한다.
이상으로 논문설명을 마치고 모델을 구현해보자.
PyTorch Implementation
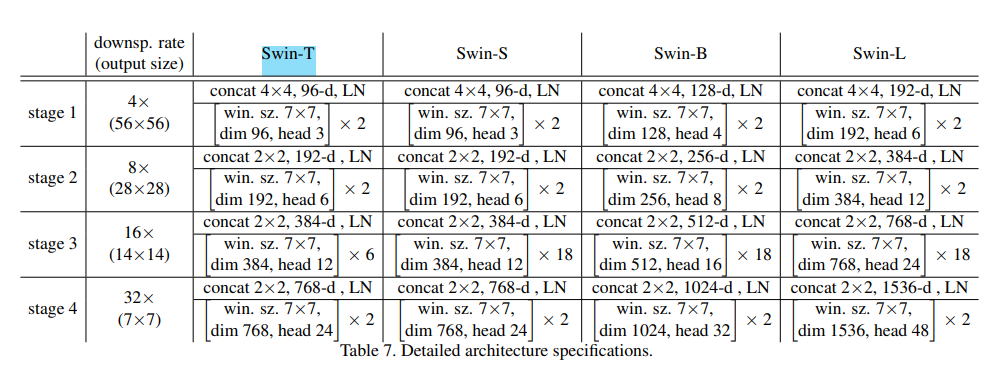
- Swin Transformer는 위와같이 4개의 모델이 있는데 그중 Swin-Tiny에 대한 구현 코드이다.
Cyclic Shift
class CyclicShift(nn.Module):
def __init__(self, displacement):
super().__init__()
self.displacement = displacement
def forward(self, x):
# x.shape (b, 56, 56, 96)
return torch.roll(x, shifts=(self.displacement, self.displacement), dims=(1, 2)) # 각 차원별로 3씩 밀어버림
- torch.roll을 사용하면 원하는 차원에 있는 값을 shift 할 수 있다.
- self.displacement = window_size // 2
Skip Connection & Layer Normalization
class Residual(nn.Module):
def __init__(self, fn):
super().__init__()
self.fn = fn
def forward(self, x, **kwargs):
return self.fn(x, **kwargs) + x
class PreNorm(nn.Module):
def __init__(self, dim, fn):
super().__init__()
self.norm = nn.LayerNorm(dim)
self.fn = fn
def forward(self, x, **kwargs):
return self.fn(self.norm(x), **kwargs)
MLP
class FeedForward(nn.Module):
def __init__(self, dim, hidden_dim):
super().__init__()
self.net = nn.Sequential(
nn.Linear(dim, hidden_dim),
nn.GELU(),
nn.Linear(hidden_dim, dim),
)
def forward(self, x):
return self.net(x)
- Encoder의 MLP구현
Mask
def create_mask(window_size, displacement, upper_lower, left_right):
mask = torch.zeros(window_size ** 2, window_size ** 2)
if upper_lower:
mask[-displacement * window_size:, :-displacement * window_size] = float('-inf')
mask[:-displacement * window_size, -displacement * window_size:] = float('-inf')
if left_right:
mask = rearrange(mask, '(h1 w1) (h2 w2) -> h1 w1 h2 w2', h1=window_size, h2=window_size)
mask[:, -displacement:, :, :-displacement] = float('-inf')
mask[:, :-displacement, :, -displacement:] = float('-inf')
mask = rearrange(mask, 'h1 w1 h2 w2 -> (h1 w1) (h2 w2)')
return mask
- cyclic shift 뒤에 수행할 마스킹 작업을 하는 함수
- 만약 window_size가 3이고 displacement가 1이라면 아래 사진에서 upper_lower 마스크는 왼쪽과 같고 left_right는 오른쪽과 같다.
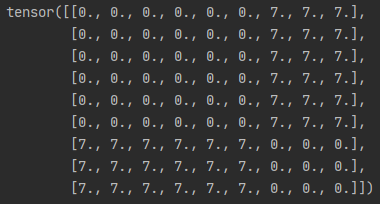
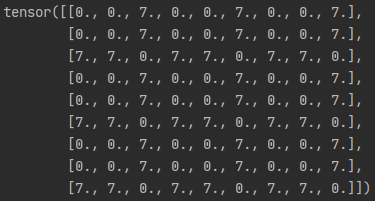
Relative Distance
def get_relative_distances(window_size):
indices = torch.tensor(np.array([[x, y] for x in range(window_size) for y in range(window_size)]))
distances = indices[None, :, :] - indices[:, None, :]
return distances
- window size를 받아서 상대거리를 반환하는 함수 ( [−M + 1, M −1] 사이의 수)
W-MSA & SW-MSA
class WindowAttention(nn.Module):
def __init__(self, dim, heads, head_dim, shifted, window_size, relative_pos_embedding):
super().__init__()
inner_dim = head_dim * heads
self.heads = heads
self.scale = head_dim ** -0.5
self.window_size = window_size
self.relative_pos_embedding = relative_pos_embedding
self.shifted = shifted
if self.shifted:
displacement = window_size // 2 # 7//2 = 3
self.cyclic_shift = CyclicShift(-displacement)
self.cyclic_back_shift = CyclicShift(displacement)
self.upper_lower_mask = nn.Parameter(create_mask(window_size=window_size, displacement=displacement,
upper_lower=True, left_right=False), requires_grad=False)
self.left_right_mask = nn.Parameter(create_mask(window_size=window_size, displacement=displacement,
upper_lower=False, left_right=True), requires_grad=False)
self.to_qkv = nn.Linear(dim, inner_dim * 3, bias=False)
if self.relative_pos_embedding:
# self.relative_indices -> index (0~12 사이의 수를 가짐) / + window_size - 1 은 음수를 없애기 위해
self.relative_indices = get_relative_distances(window_size) + window_size - 1
self.pos_embedding = nn.Parameter(torch.randn(2 * window_size - 1, 2 * window_size - 1)) # (13, 13)
else:
self.pos_embedding = nn.Parameter(torch.randn(window_size ** 2, window_size ** 2))
self.to_out = nn.Linear(inner_dim, dim)
def forward(self, x):
if self.shifted:
x = self.cyclic_shift(x)
b, n_h, n_w, _, h = *x.shape, self.heads
qkv = self.to_qkv(x).chunk(3, dim=-1) # (b, 56, 56, 288) -> tuple len 3 (b, 56, 56, 96)
nw_h = n_h // self.window_size # 8
nw_w = n_w // self.window_size # 8
q, k, v = map(
lambda t: rearrange(t, 'b (nw_h w_h) (nw_w w_w) (h d) -> b h (nw_h nw_w) (w_h w_w) d',
h=h, w_h=self.window_size, w_w=self.window_size), qkv)
# (b, 3, 64, 49, 32), (b, 3, 64, 49, 32) -> (b, 3, 64, 49, 49)
# query와 key사이의 연관성(dot product) * scale(1 / root(head_dim))
dots = einsum('b h w i d, b h w j d -> b h w i j', q, k) * self.scale
if self.relative_pos_embedding:
dots += self.pos_embedding[self.relative_indices[:, :, 0].type(torch.long),
self.relative_indices[:, :, 1].type(torch.long)] # (49, 49)
else:
dots += self.pos_embedding
if self.shifted: # masking
dots[:, :, -nw_w:] += self.upper_lower_mask # 아래쪽 가로모양 윈도우
dots[:, :, nw_w - 1::nw_w] += self.left_right_mask # 오른쪽 세로모양 마스킹
attn = dots.softmax(dim=-1)
out = einsum('b h w i j, b h w j d -> b h w i d', attn, v)
out = rearrange(out, 'b h (nw_h nw_w) (w_h w_w) d -> b (nw_h w_h) (nw_w w_w) (h d)',
h=h, w_h=self.window_size, w_w=self.window_size, nw_h=nw_h, nw_w=nw_w)
out = self.to_out(out)
if self.shifted:
out = self.cyclic_back_shift(out) # shift한 값을 원래 위치로
return out
- Transformer의 Multi head Self-Attention을 수행하는 class로 block의 두번째 encoder인 SW-MSA 에서만 self.shifted=True가 되어서 cyclic shift + mask 를 진행한다.
- relative_position_embedding을 query와 key값의 dot product를 scale로 나눈값에 더해준다.
Swin Transformer Block
class SwinBlock(nn.Module):
def __init__(self, dim, heads, head_dim, mlp_dim, shifted, window_size, relative_pos_embedding):
super().__init__()
self.attention_block = Residual(PreNorm(dim, WindowAttention(dim=dim,
heads=heads,
head_dim=head_dim,
shifted=shifted,
window_size=window_size,
relative_pos_embedding=relative_pos_embedding)))
self.mlp_block = Residual(PreNorm(dim, FeedForward(dim=dim, hidden_dim=mlp_dim)))
def forward(self, x):
x = self.attention_block(x)
x = self.mlp_block(x)
return x
- Swin Transformer를 구성하는 한개의 Encoder에 대한 구현이다.
- attention과 mlp 모두 Layer Normalization과 Skip Connection을 먼저 한다. (attention과 mlp가 뒤에 있다고 먼저 수행되는게 아님! (위에 Layer Normalization과 Residual 클래스 참고))
Patch Partition or Patch Merging & Linear Embedding
class PatchMerging(nn.Module):
def __init__(self, in_channels, out_channels, downscaling_factor):
super().__init__()
self.downscaling_factor = downscaling_factor
self.patch_merge = nn.Unfold(kernel_size=downscaling_factor, stride=downscaling_factor, padding=0)
self.linear = nn.Linear(in_channels * downscaling_factor ** 2, out_channels)
def forward(self, x):
b, c, h, w = x.shape
new_h, new_w = h // self.downscaling_factor, w // self.downscaling_factor # num patches (56 x 56)
# self.patch_merge(x) : (b, 48, 3136)
# self.patch_merge(x).view(b, -1, new_h, new_w) : (b, 48, 56, 56)
# self.patch_merge(x).view(b, -1, new_h, new_w).permute(0, 2, 3, 1) : (b, 56, 56, 48)
x = self.patch_merge(x).view(b, -1, new_h, new_w).permute(0, 2, 3, 1)
x = self.linear(x) # (b, 56, 56, 48) -> (b, 56, 56, 96)
return x
- downscaling_factor는 [4, 2, 2, 2] 로 이루어져 있기 때문에 stage1에서는 이미지가 패치로 partition 되고 그 이후 stage는 자동으로 patch merging 역할을 한다.
- Linear embedding에서 C는 각 stage에서 [96, 192, 384, 768]를 사용한다.
StageModule
class StageModule(nn.Module):
def __init__(self, in_channels, hidden_dimension, layers, downscaling_factor, num_heads, head_dim, window_size,
relative_pos_embedding):
super().__init__()
assert layers % 2 == 0, 'Stage layers need to be divisible by 2 for regular and shifted block.'
self.patch_partition = PatchMerging(in_channels=in_channels, out_channels=hidden_dimension,
downscaling_factor=downscaling_factor)
self.layers = nn.ModuleList([])
for _ in range(layers // 2):
self.layers.append(nn.ModuleList([
SwinBlock(dim=hidden_dimension, heads=num_heads, head_dim=head_dim, mlp_dim=hidden_dimension * 4,
shifted=False, window_size=window_size, relative_pos_embedding=relative_pos_embedding),
SwinBlock(dim=hidden_dimension, heads=num_heads, head_dim=head_dim, mlp_dim=hidden_dimension * 4,
shifted=True, window_size=window_size, relative_pos_embedding=relative_pos_embedding),
]))
def forward(self, x):
x = self.patch_partition(x)
for regular_block, shifted_block in self.layers:
x = regular_block(x)
x = shifted_block(x)
return x.permute(0, 3, 1, 2) # (4, 56, 56, 96) -> (4, 96, 56, 56)
- 각 스테이지는 Patch partition(merging)과 Swin Block으로 이루어져 있으며 stage3에서는 Swin Block이 세번 반복된다.
Swin Transformer
class SwinTransformer(nn.Module):
def __init__(self, *, hidden_dim, layers, heads, channels=3, num_classes=1000, head_dim=32, window_size=7,
downscaling_factors=(4, 2, 2, 2), relative_pos_embedding=True):
super().__init__()
self.stage1 = StageModule(in_channels=channels, hidden_dimension=hidden_dim, layers=layers[0],
downscaling_factor=downscaling_factors[0], num_heads=heads[0], head_dim=head_dim,
window_size=window_size, relative_pos_embedding=relative_pos_embedding)
# input shape
self.stage2 = StageModule(in_channels=hidden_dim, hidden_dimension=hidden_dim * 2, layers=layers[1],
downscaling_factor=downscaling_factors[1], num_heads=heads[1], head_dim=head_dim,
window_size=window_size, relative_pos_embedding=relative_pos_embedding)
self.stage3 = StageModule(in_channels=hidden_dim * 2, hidden_dimension=hidden_dim * 4, layers=layers[2],
downscaling_factor=downscaling_factors[2], num_heads=heads[2], head_dim=head_dim,
window_size=window_size, relative_pos_embedding=relative_pos_embedding)
self.stage4 = StageModule(in_channels=hidden_dim * 4, hidden_dimension=hidden_dim * 8, layers=layers[3],
downscaling_factor=downscaling_factors[3], num_heads=heads[3], head_dim=head_dim,
window_size=window_size, relative_pos_embedding=relative_pos_embedding)
self.mlp_head = nn.Sequential(
nn.LayerNorm(hidden_dim * 8),
nn.Linear(hidden_dim * 8, num_classes)
)
def forward(self, img):
# image shape(b, 3, 224, 224)
x = self.stage1(img) # (b, 96, 56, 56)
x = self.stage2(x) # (b, 192, 28, 28)
x = self.stage3(x) # (b, 384, 14, 14)
x = self.stage4(x) # (b, 768, 7, 7)
x = x.mean(dim=[2, 3]) # (b, 768)
return self.mlp_head(x) # (b, classes)
- 4개의 stage를 거친 후에 나오는 7x7 patch를 average pooling (mean)을 하고 최종 classifier에 넣어 예측을 한다.
Test Swin-Tiny
def swin_t(hidden_dim=96, layers=(2, 2, 6, 2), heads=(3, 6, 12, 24), **kwargs):
return SwinTransformer(hidden_dim=hidden_dim, layers=layers, heads=heads, **kwargs)
if __name__ == '__main__':
import pdb
from torchsummary import summary
model = swin_t()
x = torch.rand(4, 3, 224, 224)
outputs = model(x)
print(outputs.shape)
summary(model, input_size=(3, 224, 224), device='cpu')
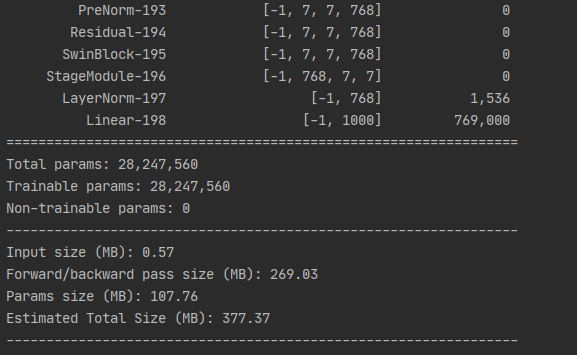
End
이번 포스팅에서는 microsoft에서 발표한 Swin Transformer에 대해 알아보았다. Swin Transformer는 hierarchical feature representation을 제시하였고 swift window를 통해 image size 증가에 대해 linear computational complexity 하게 만들었다.
현재 Image classification ImageNet dataset에서 13등까지 밀렸지만 Segmentation ADE20K dataset에서 1등 Object Detection COCO dataset에서 1등을 유지하면서 backbone network으로서의 가치를 입증하고 있다.
다음으로는 Object Detection task에서 어떻게 활용되는지 공부해봐야 겠다.
keep going.
Reference

Leave a comment